++ 50 ++ 2 次 関数 問題 109934

２次関数 ２次関数の決定について 日々是鍛錬 ひびこれたんれん

 ここでは，様々な2次関数の最大値と最小値について説明します。 2次関数の最大値と最小値を求める問題では，軸と定義域の位置関係が重要です。 様々な問題を解くことによって，2次関数の最大最小問題に慣れましょう。 Contents 1 最大値と最小値を数学Ⅰ 2次関数章末問題解答 §1 2次関数 2次関数章末問題解答ヒントと解説 1 解説 平行移動前の関数上の座標を (x,y), 移動後の点を (X,Y) とする。 すると (X,Y) は，X=x1，Y=y3 と表すことができる。 よって，x=X1，y=Y3 となる。 関連項目：1．点とグラフ

2 次 関数 問題

2 次 関数 問題-2次関数1 応用学習 グラフで迷わず場合わけ よって，①～③のそれぞれの場合について，グラフをかくと次のようになる。 1 2 練習問題の解答 ① ② ③42 x y O x x yy4 1 5323 O4 1 52 O ① ② ③ x 12 2 3 y O 111 1 3 y O x PMT4E1Z1N301 0 ＜ a ≦ 3 のとき 最大値； 2－ a 二次関数の決定の問題は、与えられた条件に応じて解き方を変えましょう。 Tips 頂点 \((p, q)\) または軸 \(x = p\) が与えられた場合 → \(\color{red}{y = a(x − p)^2 q}\) とおく！ 関数が通る \(3\) 点が与えられた場合 → \(\color{red}{y = ax^2 bx c}\) とおく！ あとは、連立方程式のように未知の係数を求め

数1二次関数です 1 についての質問です Clearnote

2次方程式の活用(2) 2次方程式の活用(3) 4 関数 y 問題一括 (2,462Kb) 解答一括 (2,734Kb) 円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の 数学Ⅰ 2次関数 最大・最小特訓④ ＜定義域が動く＞ 問題編 数学Ⅰ 2次関数 最大・最小特訓④ ＜定義域が動く＞ 解答編 2次関数の決定 ＜頂点・軸・3点を通る＞ 数学Ⅰ 2次関数 2次関数の決定特訓① ＜軸・頂点・3点＞ 問題編 数学Ⅰ 2次関数 2次関数の 数学3．関数 3．二次関数 2．二次関数の変化の割合・変域 数学3．関数 3．二次関数 3．二次関数の座標・グラフ・式 数学3．関数 3．二次関数 4．二次関数と図形関連の複合問題

問題4 2次関数 の頂点、および x軸との交点の座標を求め、グラフを描け。 問題5 次の放物線の方程式を求めよ。 (1) 頂点が(2, 4)で、点(1, 3)を通る。 (2) 点(1, 1) (1, 3) (2, 7)を通る。 (3) 点(3, 0) (2, 0)を通り(1,8)を通る。 問題6 の係数が1で、頂点が 上にあり、点(5,12)を通る放物線の方程式を求No17 2次方程式① 問題 の答え 誤「865」⇒ 正「866」 定期テスト数学対策 中3分野 「2乗に比例する関数 」の1 関数 u = 2x2 4x 2 微分 u0 = 4x4 = 4(x 1) 3 Fermat u0 = 0, 4(x 1) = 0) ∴ {x = 1 y = 2 問2 次の最適化問題を1変数関数の極値問題にブレイクダウンすることによって、解きなさい。 最大化 u = x2y 条件

2 次 関数 問題のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	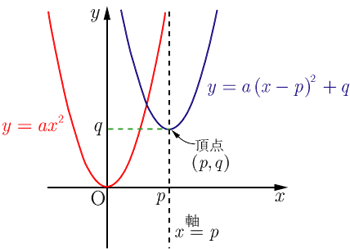2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	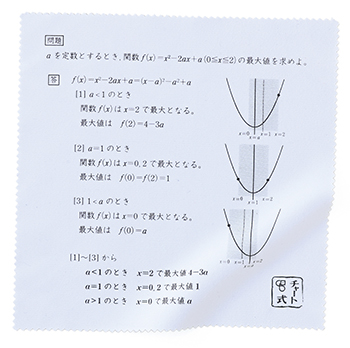2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx	2次関数 媒介変数 スタディーx
2次関数 媒介変数 スタディーx	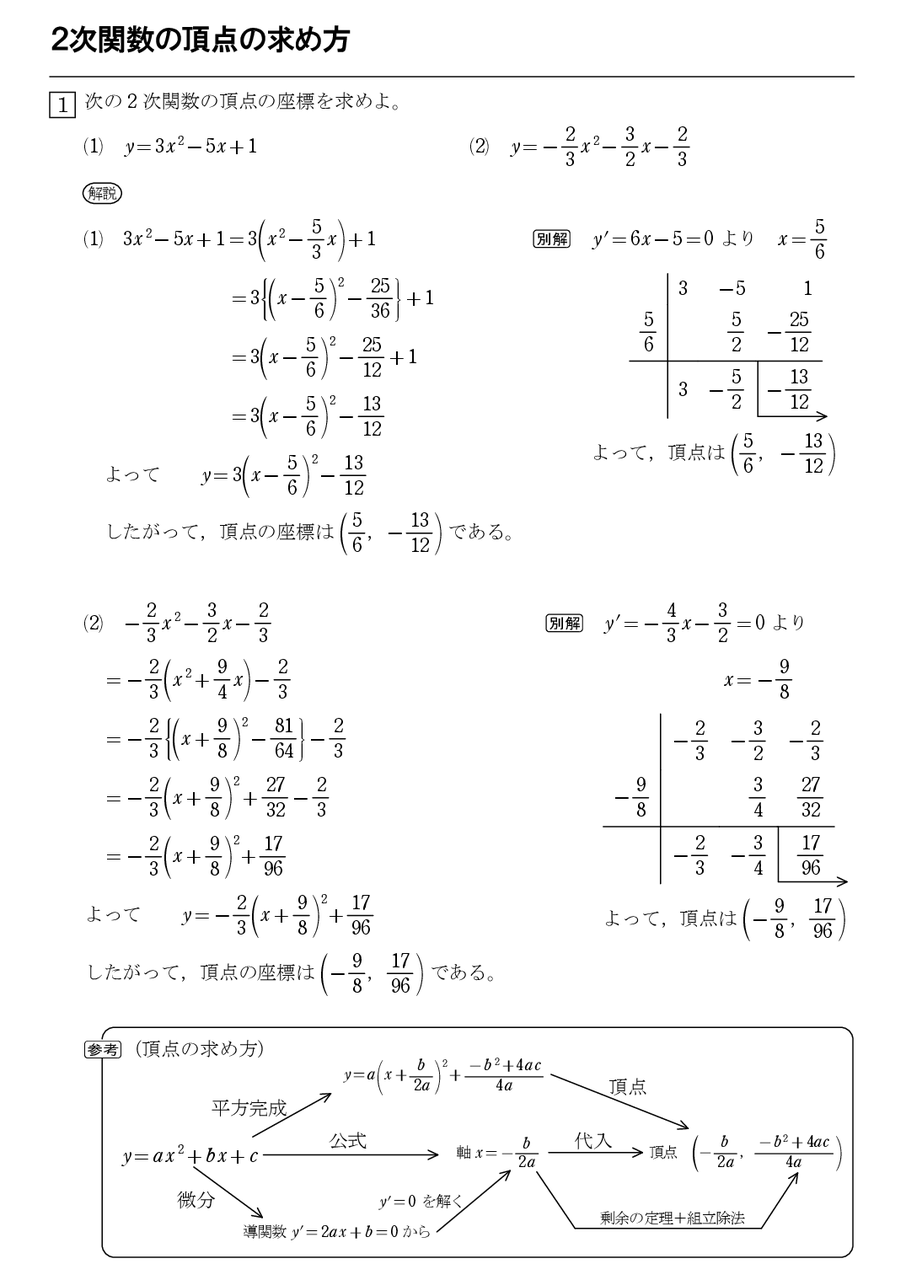2次関数 媒介変数 スタディーx

 アレを教えるかどうかで議論された問題。 ・1次関数と図形座標（★★★★★）（14年度洛南） 塾講師や数学教師が教えたい要素たくさん。 ②，2次関数グラフ ・無数の解法関数（18年度三重県）（？？？？？） シンプルな見た目して，たくさんの別解が2次関数⑥「最大値、最小値の考え方」 2次関数⑦「場合分けの必要な最大値、最小値問題」 2次関数⑧「場合分けの必要な最大値、最小値問題 その2」 2次関数⑨「解の配置に関する問題」 数列のシグマの問題 数列のシグマに関する問題を作成しました。